Preamble
System error budgets should be developed and analyzed
as an integral part of system designs. System engineers
must determine the necessary levels of accuracy for
system elements such as field sensors, actuators, signal
conditioning modules (SCMs), and controlling units (PCs
and PLCs). In addition, software algorithm integrity and
operating system compatibility, or the degree of software
“openness,” must be included in error budget
considerations. For example, the accuracy and resolution
of software algorithm calculations must be compatible
with measurement accuracy.
In the process of analyzing system accuracy needs, the
topic of resolution requires attention as it relates to overall
accuracy. Oftentimes distinguishing between accuracy
and resolution is misinterpreted in determining system
needs. Some examples and illustrations are presented in
this Application Note in an attempt to show readers that
there is a significant difference between accuracy and
resolution, even though they are related.
Examples
Before launching into some examples, recall how
accuracy is denoted. A reading device that has a specified
accuracy of ±0.015% will actually give a reading that is
between 0.99985 and 1.00015 times the actual value.
Interesting how our standards have defined “accuracy.”
Note here that the ±0.015% number is in reality the
“error.”
Accuracy is the measurement device’s degree of absolute
correctness, whereas resolution is the smallest number
that can be displayed or recorded by the measurement
device. For example, measuring 1 volt within ±0.015%
accuracy requires a 6-digit instrument capable of
displaying five decimal places. The fifth decimal place
represents 10 microvolts, giving this instrument a
resolution of 10 microvolts.
For the following examples, the digital display quantizing
error (±1 bit minimum) in the least significant digit is
assumed to be zero.
Example 1
Suppose one has a voltage source that is known to be
exactly 5.643 volts. Now imagine, if you will, that one
uses a digital voltmeter that is (somehow) 100% accurate,
but has only 3 display digits and is defined as “3-digit
resolution.” The reading would be 5.64 volts. Is the
reading accurate? There was an accurate source and an
accurate voltmeter, yet the reading does not represent the
actual voltage value. Some may say that our 100%
accurate voltmeter gave us a reading error of 3 millivolt
or 0.0532%.
In this hypothetical example, the reading could be
considered in error unless one only wants a 3-digit
reading. In cases where source and instrument accuracy
are 100%, the resolution of the reading instrument and the
acceptance of the observer determine what constitutes
“accuracy.”
Example 2
Again assume a 100% accurate source of 5.643 volts;
however, in this case our 3-digit display digital voltmeter
has a ±0.015% accuracy specification (recall this means
that the displayed value is actually between 0.99985 and
1.00015 times the source value).
In this case, the digital voltmeter still reads 5.64 volts.
One can say that this 0.015% accurate instrument gives a
0.0532% error, as in Example 1. Once again, the
resolution and the observer determine what constitutes
“accuracy.”
Example 3
In this example, consider measuring the precise 5.643-
volt source using a 5-digit display digital voltmeter with a
specified accuracy of ±0.015%. This instrument displays
a reading of between 5.6421 (for 5.64215) and 5.6438 (for
5.64385).
Example 4
Repeat Example 3 using a 6-digit display digital
voltmeter, again with a specified accuracy of ±0.015%.
The display will be between 5.64215 and 5.64385.
Clearly, these examples illustrate that accuracy and
resolution are indeed related, and each situation has to be
evaluated based on the system requirements and the
observer’s acceptance of “error.”
Reality
A typical situation is illustrated in Figure 1. As shown,
sensor signals are conditioned with signal conditioning
modules, selected, and then converted into a usable
number either for analytical process control or
observation.
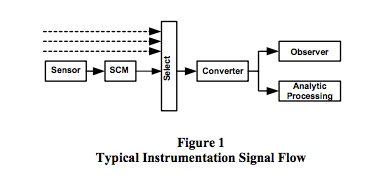
In Figure 1, assume sensors have ±0.25% (E1) accuracy
specifications, SCMs have ±0.03% (E2) accuracy
specifications, and the select-converter function has
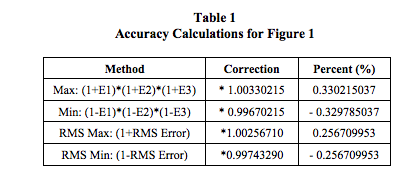
±0.05% (E3) net accuracy. Table 1 displays some
different system “accuracy” correction calculations. Since
errors are random and have ± values, RMS calculations
are often used as opposed to the worst case maximum and
minimum. RMS error is defined as the square root of the
sum of each error squared, √ {(E1)2 + (E2)2 + (E3)2 }.
Number values from the converter function in Figure 1
are presented to the observer with a display unit that has
its own error and resolution specifications. In addition, the
analytical processing function imports this numerical
value to use in a complex mathematical operation, which
may be based on an empirical model that achieves results
using computation shortcuts, which in turn have
additional accuracy and resolution specifications.
As is evident, a detail error budget must contain numerous
factors in order to correctly determine “system accuracy.”
Reality Check
Have you ever experienced this scenario or one similar?
Your project manager wanders into your office
(cubicle), makes small talk about how the
control system project is going, and asks if you
and your team have any needs. Before leaving,
he comments that while reviewing your project
purchases he noticed that the ADC module for
the main controller is an 8-channel differential
input unit with 16-bit resolution, which he
thought would give one part in (216 -1) accuracy,
something on the order of 0.0015%. He says he
also noticed that all the SCMs you purchased
were only 0.03%. Politely, he asks you to
explain. You begin your explanation by
pictorially representing one possible ADC
system, as illustrated in Figure 1.
Analog-to-digital converters (ADC) are advertised as
having “n” bit resolution, which often is misunderstood to
mean accuracy. Specifications need to be closely
examined, however, to determine the unit’s true accuracy.
Figure 2 depicts one typical scheme used to convert an
analog signal to a digital representation for computer
manipulations or display. In this typical representation,
semiconductor switches select analog input signals, which
are captured (sampled for a small slice of time) and held
in a sample and hold amplifier function block (SHA).
This SHA function may also contain a programmable gain
function to selectively scale each analog input. Once a
signal slice is captured, an n-bit counter begins to count.
The counter contents are converted to an analog voltage
using switched resistors or current sources. When this
analog signal equals the input SHA signal, counting halts
and the counter contents are made available as a digital
representation of the sampled analog input value. This
process can sample analog inputs at blinding speeds in the
10MHz range to provide digital representations of time
varying analog inputs; it also has numerous sources of
error that collectively degrade true accuracy, which is not
necessarily determined solely by the n-bit resolution
specification.
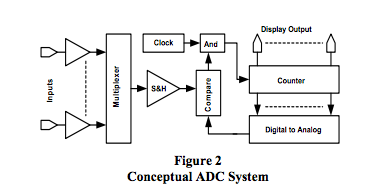
ADC Error Budget
The following list identifies errors associated with using a
typical ADC scheme such as illustrated in Figure 2.
- Sampling Speed
From Nyquist Sampling Theory, if the analog signal
changes rapidly, then the ADC must sample at least
twice as fast as the changing input. Many applications
use a sampling rate at least 10 times the highest
frequency present in the input signal. Sampling slower
than one-half the signal frequency will result in
inaccurate readings. Most ADC’s sampling speeds are
adequate for slow varying process control signals.
See Reference 2 for more details on this topic.
- Input Multiplexed Errors
The input multiplexer circuit may have OpAmp
buffers on each input line that could introduce errors
such as in voltage offset, current bias, and linearity. In
addition (and more common) are the two major
multiplexer errors: (a) cross talk between channels,
i.e., the signal from an “on” channel leaks current into
the “off” channels, and (b) signal reduction through
voltage division caused by the finite non-zero
resistance of the semiconductor switches and the finite
input impedance of the circuitry that follows.
- Sample and Hold Amplifier (SHA)
This function is an OpAmp based circuit with
capacitive components all designed to switch, buffer,
and hold the sampled analog voltage value.
Consequently, there will be linearity, gain, powersupply
rejection ratio (PSRR), voltage offset, charge
injection, and input bias current errors. For a detail
analysis of typical OpAmp errors, see Dataforth’s
Application Note AN102, Reference 3.
- Converter
In the counter, comparator, and ADC circuit there are
such errors as overall linearity, quantizing error
(defined as uncertainty in the least significant bit
[LSB], typically ±1/2 LSB), and PSRR.
- Temperature
All analog circuit functions within the ADC unit are
subject to temperature errors and hence an overall
temperature error specification is assigned to an ADC.
Table 2 identifies some of the internal errors associated
with a typical ADC. Data was taken from various analogto-digital
converter manufacturers. This table is by no
means a complete ADC error analysis; the values shown
illustrate that there are internal errors that collectively
contribute to the definition of an ADC’s overall accuracy.
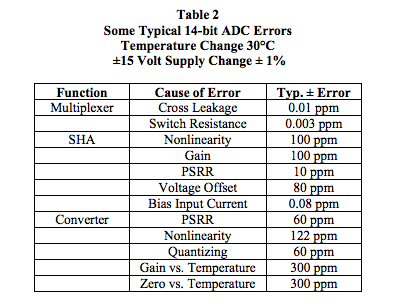
An algebraic sum model on these errors suggests a ±0.1%
error for this 14-bit ADC, whereas the RMS sum model
suggests a ±0.05 % error. Resolution alone erroneously
implies ±0.006%. These internal ADC error numbers used
in either an algebraic or RMS summing model clearly
illustrate that the net effective accuracy of an n-bit ADC
is not equal to the ADC resolution, defined as
approximately 1/(2n -1). To determine actual ADC
accuracy, the manufacturer’s ADC specifications should
always be carefully examined.
Note: Industrial sensors used in process control and data
acquisition systems can have accuracies that are much
less than SCMs or ADC units and often dominate errors
in a total system error budget. Dataforth SCMs have
accuracies that typically exceed both those of industrial
sensors and ADC modules. Readers are encouraged to
examine Dataforth’s complete line of SCM products. See
Reference 1.
Dataforth References
- Dataforth Corp. Website
http://www.dataforth.com
- Dataforth Corp., Application Note AN112
http://liwww.dataforth.com/technical_lit.html
- Dataforth Corp. Excel Interactive Workbook
for 2-Pole LP Active Filter
http://liwww.dataforth.com/catalog/pdf/an113.xls