Preamble
When we purchase electrical equipment,
appliances, light bulbs, motors, heaters and
such, somewhere on the “name plate” are some
electrical specifications such as voltage, current,
frequency, power, etc. We have seen these
values for as long as we have been able to read
and so we just take them for granted. For AC
(the abbreviation for alternating current), the
values for voltage and current are always shown
as “RMS” values; however, this fact is rarely
stated on the name plate. It is assumed everyone
knows this.
What does RMS really mean? This Application
Note will revisit the definition of RMS, show
RMS values for various time functions, and
explore some interesting RMS measurement
issues. Our object here is to provide a better
understanding of some of the subtle
characteristics of RMS. However, reviewing
RMS values for time functions containing
random components is beyond the scope of this
Application Note.
The Appendix contains additional information
for your reference, and the reader is encouraged
to examine the previous Dataforth Application
Note on RMS, AN101.
RMS Definition Revisited
Throughout this Application Note, we will
consider only periodic functions with no random
components. The way to think of the RMS value
for a time varying function of voltage or current
is to recognize that an RMS value for these time
varying items means that the time varying
function has the same energy capacity as some
value of DC (abbreviation for direct current)
voltage or current.
The derivation of RMS begins with the
requirement that the function of time is “well”
behaved (bounded with a finite number of
discontinuities), repetitive at some fundamental
frequency, and available for as long as needed.
A pure mathematician might cringe at these
simple requirements but we engineers love them
because they apply to most types of voltages
and currents we deal with in practice.
The experimental apparatus is a pure resistive
heating element within a perfectly thermally
insulated container. An ideal DC voltage (say 10 volts) is connected to this heater until thermal
equilibrium is reached with a final temperature
of say Tx degrees.
Next, this DC voltage is removed, the unit is
allowed to cool down, and a time varying
voltage, V(t), is applied to the heater until
thermal equilibrium is again reached with a final
temperature of, say, Ty degrees. If Ty = Tx,
then the effective value of V(t) = 10 volts (same
as the previous DC value) and so we say the
RMS value of V(t) is effectively 10 DC volts.
Why the name RMS? The name comes from the
mathematics of this experiment as follows:

A careful look at this mathematical equation
shows that it is the Root of the Mean (average)
value of V(t) Squared. Hence, the name RMS.
RMS Examples
Perhaps the most familiar time function is the
sinusoidal function. Recall that a sinusoidal
function can be described as a sine function or
cosine function depending on where we choose
to place the time origin. As you know, the utility
companies go to great lengths to ensure the
voltage on their power grid distribution system
is a sinusoidal voltage function. Consequently,
the RMS value of sinusoidal functions of time is
the dominant focus in most introductory electric
circuit courses and little time is spent on determining RMS values for unusual shaped
functions of time.
Most of us recall the RMS of a sinusoidal
function as:
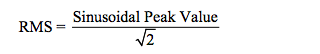
For example, consider the name plate
specifications of a toaster showing 120VAC,
60Hz. This means the actual utility line voltage
out of the wall socket is a 60Hz sinusoidal
voltage function with a peak value of 169.7
volts. This utility supply voltage function of
time is commonly expressed by either of the
following sinusoids:
v(t) = 169.7*Sin(2*π*60*t)
v(t) = 169.7*Cos(2*π*60*t)
All this is well and good but the fact is there are
scores of other functions of time that we need to
measure that are nowhere near sinusoidal. So
what about these? As an example, consider nonlinear
loads on the utility’s fixed sinusoidal
voltage line; the load currents will in no way be
sinusoidal but we need to measure them
nonetheless.
Table 1 (page 7) illustrates some common nonsinusoidal
time functions and their associated
RMS values. Take a look, you may be surprised.
Parceval’s Theorem
Parceval’s Theorem is a handy trick to know.
As an illustrative example of using this theorem,
consider the situation where an auxiliary
emergency backup generator is connected to a
facility. It is possible for such generators to
create sinusoidal harmonics on the customer’s
supply lines. Sometimes such generator’s
specifications give the harmonic content.
Figure 1 illustrates a situation where the
composite voltage is a sum of four different RMS voltages, one at a fundamental frequency,
one at the third harmonic, one at the fifth
harmonic, and a DC average.
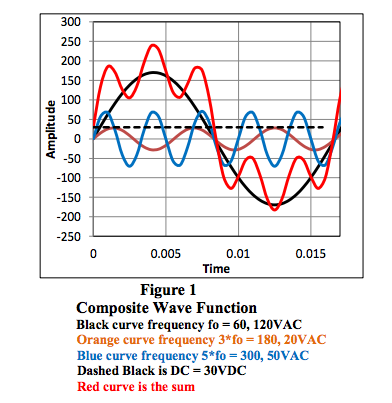
So what is the RMS value of the RED function
of time? Do you want to write an equation for it
and use Eqn. 1? Well, we could but it would be
messy so instead let us use Parceval’s Theorem,
which says that for a composite function
composed of different functions, the RMS value
can be calculated by the following:

We will show more practical examples of
Parceval’s Theorem later on when we use the
Fourier Series to calculate RMS.
Measuring RMS
Any module that measures the RMS value of a
time varying function must, in general,
implement Eqn. 1 (page 2). The modern
techniques and circuit topologies of such
devices are far beyond the scope of this
Application Note. Moreover, most vendors of
such devices consider their methods to be
intellectual property (IP) and do not publicize
their circuits and embedded software (if any).
Companies that supply RMS modules use
various implementations of Eqn. 1 ranging from
simple analogy circuit topologies to
sophisticated digital sampling with Digital
Signal Processing (DSP) microprocessors
running special software algorithms. However,
as a selection aid, device specifications are
always provided.
For example, Dataforth RMS Measurement
Modules provide specifications that include:
- Component Drift
- Component Aging
- Temperature Variation
- Supply Voltage Variation
- Humidity
- Circuit Linearity
- Circuit Repeatability and Hysteresis
- Common Mode Voltage Rejection
- Transient Protection
- Frequency Response
- Crest Form Factor
Most readers are familiar with the analog
specifications 1-9 and how they apply to their
specific requirements; therefore, we will not
dwell on these in this Application Note.
However, Frequency Response and Crest Factor
(Form Factor) specifications may need a little
additional examination.
Non-Sinusoidal Measurement Example
As a typical example of a non-sinusoidal time
function, consider the situation in which a 60Hz
utility supply is connected to a non-linear load.
We will use for illustration purposes a full wave bridge rectifier as the non-linear load. Industrial
facilities have speed drive for induction motors,
controllers for DC motors, welders, and large
dimmer units. In general, all these have within
their circuit topology some form of AC to DC
converter and may or may not have an input line
filter.
Figure 2 shows the typical wave forms in this
situation.
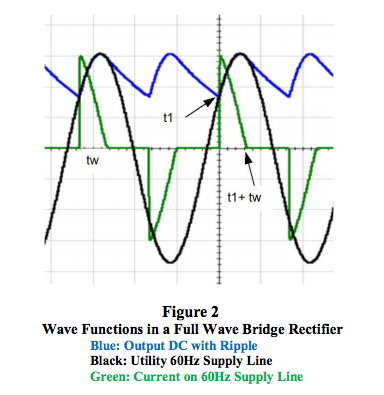
Notice that the output is a DC voltage with a
rippling value at 120Hz riding on top of an
average (DC) value. Perhaps most surprising is
the green line current pulse shaped like a sawtooth
with a frequency at twice the line
frequency, 120Hz. So what is the RMS value of
this current pulse?
The Fourier Series
Recall Fourier’s theorem, which says that a
function of time “f(t)” can be expressed as a
sum of sine and cosine functions over an infinite
number of frequencies plus an average value
term. At this point, a mathematician would
hasten to give us all the limitations for this
theorem; however, most engineering voltages and currents we work with are “well” behaved
and Fourier’s theorem applies. The following
form of this theorem will allow us to
demonstrate the effects of frequency on RMS
measurements.
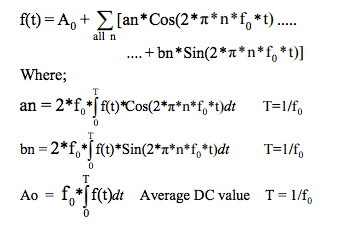
Note that “f0” is the signal “f(t)” frequency and
that “an” is the peak amplitude of the “nth”
Cosine harmonic and “bn” is the peak
coefficient of the “nth” Sine harmonic.
Remember that a non-sinusoidal time function
contains many (infinite number in theory)
different frequency harmonics. We can use this
fact to calculate the RMS of non-sinusoidal time
functions by using Parceval’s Theorem for
RMS, which is:
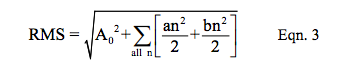
Recall, RMS is Vpeak ÷ square root 2.
We hasten to point out that all this is interesting;
however, the shape of a time function whose
RMS value we wish to measure is seldom, if
ever, known. So what is the value of this nasty
math? From a practical point of view we rarely
use this analysis to actually calculate RMS since
the equation for the quantity we wish to measure
is unknown. However, we are going to use this
analysis in examples to illustrate the frequency
requirements of measuring non-sinusoidal
functions and therein lies the value of this nasty
math.
Example 1
Figure 2 (page 4) shows the actual 60Hz line
current in typical industrial equipment
containing bridge rectifiers. This green line
current approximates a sawtooth wave form.
To partially simplify the mathematical
calculations, we will model this sawtooth
function as:
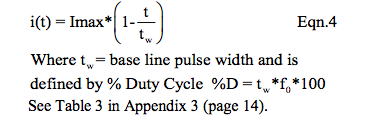
The pulse shape and specifically the pulse width
“tw” is determined by the load resistance, the
filter capacitance, and the supply frequency.
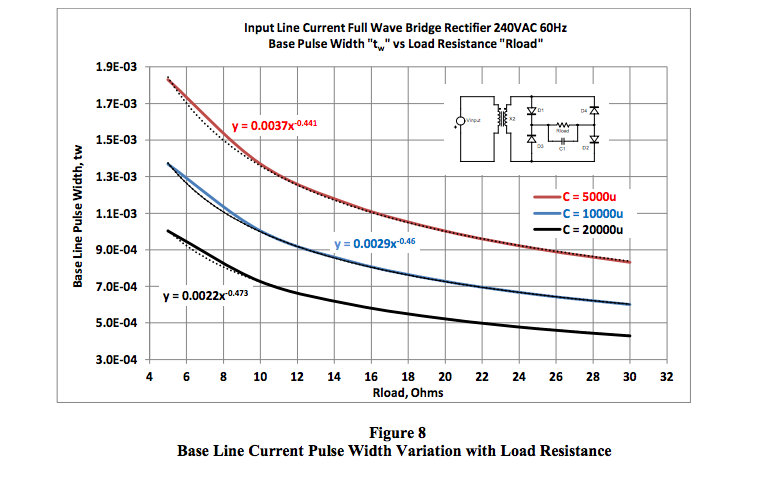
Figure 8 (Appendix 2, page 13) shows an
example of how pulse widths can vary with load
resistance for several given filter capacitances.
The model used here (shown above) is
sufficiently accurate to illustrate our objective,
which is to show the effects of frequency
content in this common type non-sinusoidal line
current. Remember that “f0” is the driving
source frequency (60Hz in this example) not the
pulse frequency.
Reexamine the bipolar sawtooth line current
function shown as green in Figure 2. The graph
in Figure 4 (page 8) illustrates how RMS
%Error as a function of base line pulse width
expressed as Duty cycle varies with different
“n” numbers, i.e. frequency components.
Note Results in Figure 4
1. For any given number of frequency
harmonics (n value) the RMS %Error
decreases as %D increases, that is as tw
increases RMS %Error decreases for any
given n.
2. For any pulse width tw given as %D, the
RMS %Error decreases as number of
frequency harmonics (n) increases.
The nasty math in this example shows the 60Hz
line current RMS %Error for 30 %D and 300
frequency components is -0.0845%. However,
to achieve this accuracy (at 30 %D and n = 300)
requires the measurement device to have a
frequency response in excess of 18,000Hz
(60*300).
Example 2
The second entry #2 of Table 1 (page 7)
illustrates a Positive Pulse Train with a fixed
frequency and varying base line pulse width.
This sort of time function is analogous to a
pulse width modulation (PWM) device used in
such applications as load dimmers, and speed
controllers, etc. Although such devices are more
complex than this simple example, it is adequate
to illustrate our objective, which is to show
another example of how RMS values are
dependent on pulse width and frequency
content. The results of this analysis are very
similar to the analysis in Example 1. Examine
Figure 5 (page 9) and notice again how RMS
value depends on the frequency content of the
measured pulse train.
Example 3
Consider a half-wave rectified sine wave as
shown in blue for the #6 entry of Table 1 (page
7). It is clear that the time function is just the
positive half of a sine wave at some frequency,
“f0”. In addition we see that this function does
not have sharp corners with varying base line
widths; therefore, we intuitively suspect that the
frequency content (harmonics of f0) will be
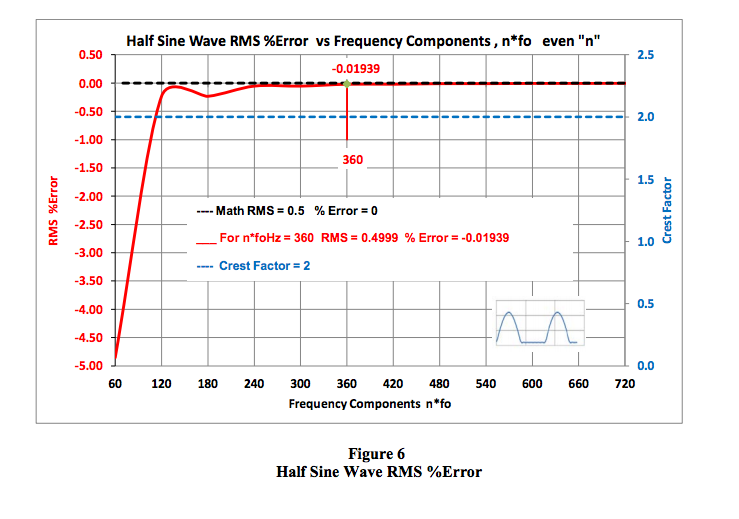
small. Figure 6 (page10) clearly illustrates this.
Similar results apply to the Full Wave Rectified
Sine Wave, entry #7 in Table 1.
Another Surprise Example
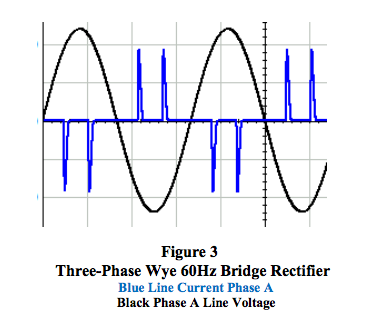
Consider the case where a 50 horsepower DC
motor is driven by a 60Hz three-phase balanced
Wye AC to DC speed controller containing a
non-line filtered bridge rectifier. We want to
measure the RMS phase line current in one
60Hz phase voltage line.
Figure 3 for this proposed situation shows in
blue the three-phase line current in phase A. Is
this a surprise? Can your RMS measurement
device correctly measure RMS values of this
type 60Hz line current?
Equations
Appendix 1 (page 12) displays Fourier Series
equations for examples used in this Application
Note.
Crest Factor
Another interesting specification on RMS
measurement modules is the Crest Factor,
sometimes called the Form Factor. Error due to
Crest Factor is an often stated specification for
RMS measurement devices. Crest Factor is
defined as:
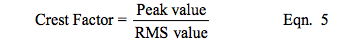
Using the Crest Factor specification as a
selection guide requires that one knows both the
peak amplitude value and the RMS value of the
time function to be measured. Unfortunately
both are unknown before measurements are
made. Therefore, it is essentially impossible to
specify an RMS error associated with the Crest
Factor for all possible non-sinusoidal time
functions. Nevertheless, RMS measurement
module suppliers do show a range of Crest Factor errors that a buyer can use to get a
“handle” on possible RMS errors caused by
non-sinusoidal shaped time function for a given
RMS measurement application.
The Conclusion
The above examples illustrate that when
measuring RMS one should try to determine
what is being measured and make sure the RMS
measurement device has adequate frequency
response, in excess of n*f0. This may be
somewhat difficult to do accurately since one
does not usually know beforehand the shape of
the signal to be measured and exactly how many
(“n”) harmonic frequencies are necessary to
achieve a required accuracy in the RMS
measurement.
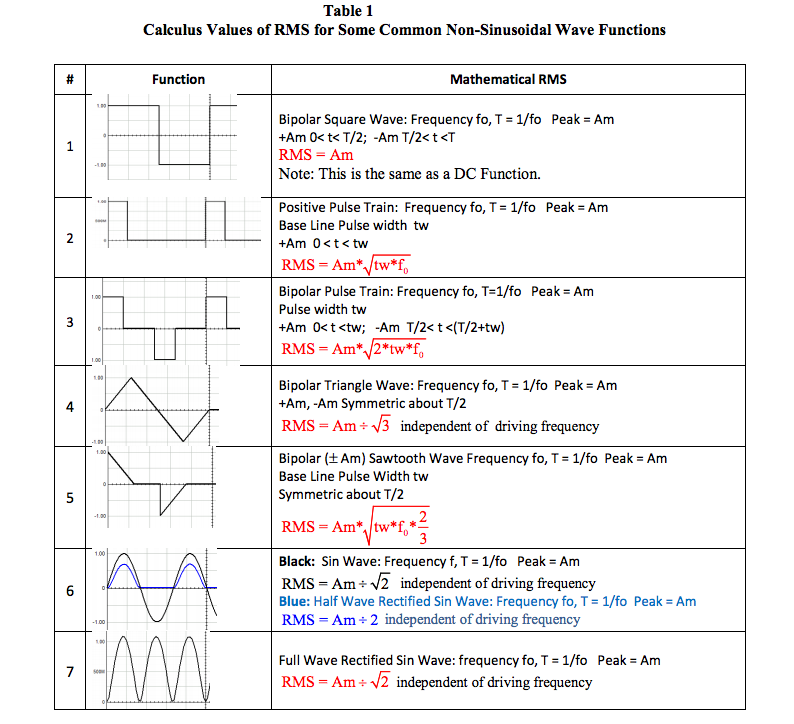
The graph shown below in Figure 4 is a sample illustration of how the RMS error value of a sawtooth
bipolar pulse varies with base line pulse width (tw) expressed in % Duty Cycle and number (n) of
harmonic frequency components. In addition, the variation in Crest Factor is shown.
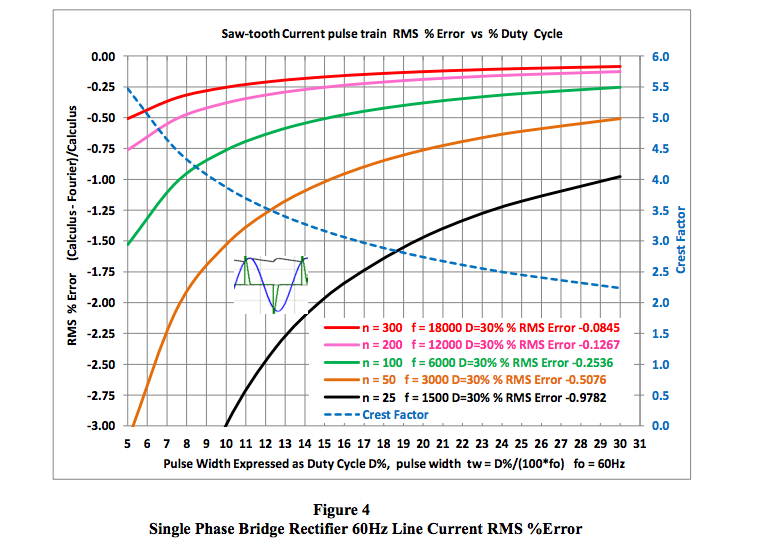
The graph shown below in Figure 5 is another sample illustration of how the RMS error value of a
non-sinusoidal rectangular positive pulse train wave form varies with base line pulse width (tw)
expressed in % Duty Cycle and number (n) of harmonic frequency components. Pulse trains of this
nature are analogous to pulse width modulation, PWM devices. In addition, the variation in Crest
Factor is shown.
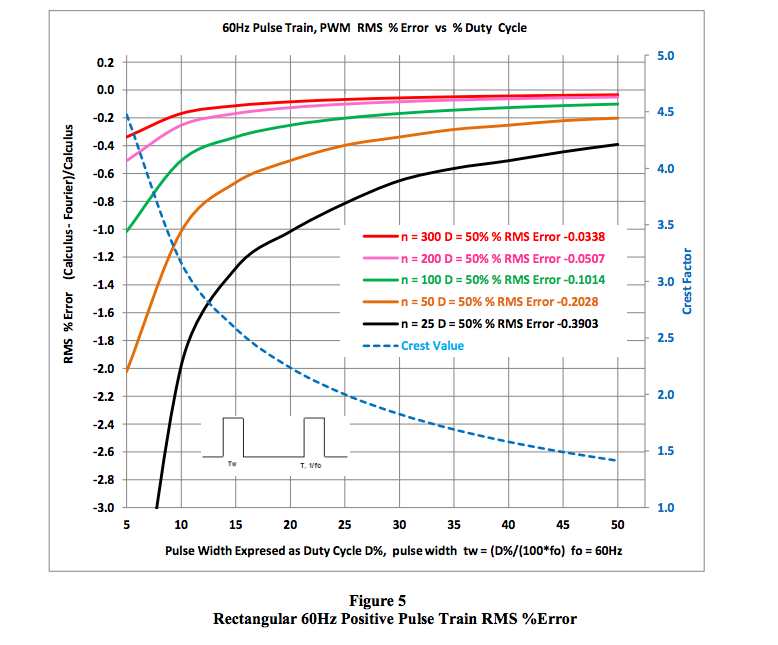
The graph shown below in Figure 6 is a special example of how the half wave rectified Sine wave
RMS error value varies with the number (n) of harmonic frequency components. As shown, a
relatively small number of harmonic frequency components (three in this graph) is required to
establish a tiny RMS %Error. This is expected, since the pulse width is exactly half a period and the
function is a smooth completely defined sinusoid. In addition, the Crest Factor is shown as a constant
value of two.
DATAFORTH RMS MEASUREMENT DEVICES
True RMS measurements require instrumentation devices that accurately implement the RMS
equation. Dataforth has developed three RMS module families that do just that: the SCM5B33,
SensorLex® 8B33, and DSCA33. All three families are made up of isolated True RMS input
modules that provide 1500Vrms transformer isolation. Each module provides a single channel of
AC input that is converted to its True RMS DC value, filtered, isolated, amplified, and converted
to standard process voltage or current output (Figure 7 below).
The SCM5B33 and SensorLex 8B33 are plug-in-panel products; the DSCA33 is a DIN rail mount
device.
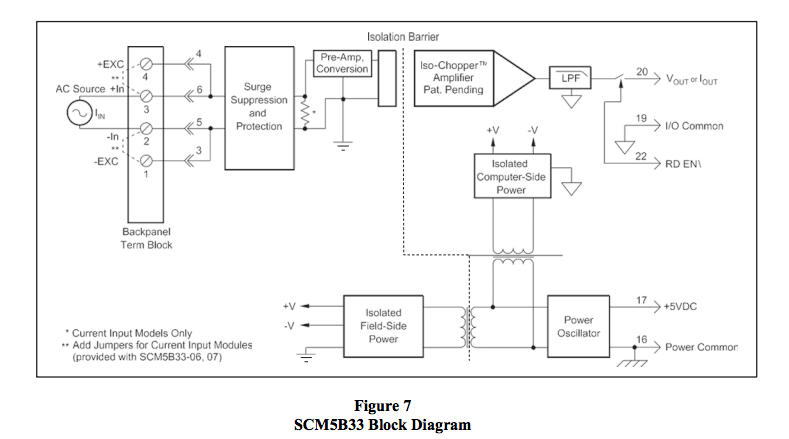
Block diagrams for the 8B33 and DSCA33 are very similar to the 5B33.
References:
- Dataforth Corp., http://liwww.dataforth.com
- Dataforth AN101 Measuring RMS Values of Voltage and Current,
http://liwww.dataforth.com/catalog/pdf/an101.pdf
Appendix
Appendix.1
Fourier Series equations for examples in this Application Note are shown below for your reference.
Recall for all time periodic well behaved functions “f(t)” the Fourier Series representation is:
- f(t) = ao + n over all “n” for [ an*Cos(n*2*π*fo*t) + bn*Sin(n*2*π*fo*t]
- “n” is the number of a particular frequency harmonic, n = 1 to infinity is the limit
- “fo” is driving source frequency, T = 1/fo
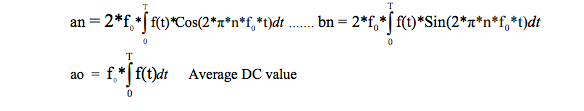
- Fourier RMS = {ao^2 + n over all “n” for [(an^2 + bn^2)/2]}^0.5
- Calculus Crest Value = Am ÷ RMS Value Where Am is Amplitude maximum = Vpeak
1a. Bipolar Square Wave, #1 in Table 1
an = 0
bn = (2*Am/(Pi*n))*(1-Cos(π*n)) n is odd; no even harmonics
ao = 0
2a. Positive Pulse Train, #2 in Table 1
an = (Am/n*Pi)*Sin(2*π*n*fo*tw)
bn = (Am/n*Pi)*(1-Cos(2*π*n*fo*tw ))
ao = Am* tw *fo
3a. Bipolar Pulse Train, #3 in Table 1
an =(Am/n*Pi)*Sin(2*π*n*fo*tw) *(1 – Cos(n*π))
bn = (Am/n*Pi)*(1-Cos(2*π*n*fo*tw )) *(1 – Cos(n*π))
ao = 0
4a. Triangle Wave, #4 in Table1
an = 0
bn = (Am*8/(π^2*n^2))*Sin(n*π/2) n is odd; no even harmonics
ao = 0
5a. Bipolar Sawtooth Wave, #5 in Table 1
an = (Am/(2*fo* tw *π^2*n^2))*(1-cos(n*2*π*fo* tw ))*(1-cos(n*π))
bn = (Am/(n*Pi) - (Am/(π^2*fo*n^2*2* tw ))*sin(n*2*π*fo* tw )))*(1-cos(n*π))
ao = 0
6a. Half Wave Rectified Sin Wave, #6 in Table 1
an = (-2*Am/(π*(n^2-1)) n is even
b1 = Am/2 n =1
bn = 0 for all n > 1
ao = Am/Pi
7a. Full Wave Rectified Sin Wave, #7 in Table 1
an = (-4*Am/(π*(n^2-1)) n is even
bn = 0 for n >1
ao = 2*Am/Pi
Appendix 2.
Some interesting results are shown below in Figure 8. Given our ideal model (Equation 4) of a
sawtooth line current pulse train, the empirical data shown in Figure 8 illustrates the variation trend in
base line pulse width (tw) with load resistance for various values of filter capacitance.
Appendix 3.
Table 3 shown below illustrates a comparison between the assumed ideal model of a current
sawtooth pulse used in this Application Note to analyze a full wave bridge rectifier and a PSpice
simulation of an actual bridge full wave rectifier. Although the individual results are not identical,
the comparisons are close enough to justify the ideal model used for our Fourier Series analysis.
Remember that PSpice simulation uses real models for circuit elements whereas our model uses
ideal components.
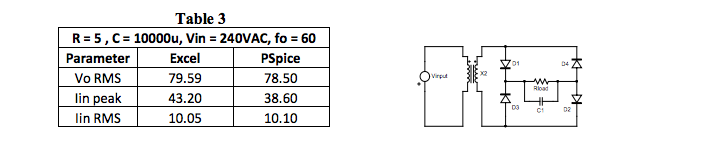
Appendix 4.
The output of a full wave rectifier with a capacitor filter has both a DC value and a ripple component
determined by the input AC RMS voltage, input driving frequency, and the rectifier circuit
components such as filter capacitance and load resistor. See Figure 2 (page 4) for a reference.
Using Parceval’s Theorem we could determine the output RMS value. Unfortunately, we do not know
beforehand the individual RMS values of the DC and Ripple component. You may find interesting the
equations shown below, which represent an analytic effort to calculate the output RMS voltage and
the peak current occurring at the instant the filter capacitor begins to charge. The following equations
are derived using our Excel model, (Equation 4 page 5). Table 3 above illustrates the comparison
results.
4a. VoRMS = [(Vin*2^0.5)*((Rload*C*fo*(1-EXP(-2*t1/(Rload*C)) + 0.5
- (1/(4*π))*Sin(4*π*fo*t1))^0.5)]/X2
4b. Ipeak = ((VinRMS/X2)*2^0.5)*(C*2*π*fo)*Sin(2*π*fo*t1) +
(-VinRMS/X2)*2^0.5)*Cos(2*π*fo*t1))/(Rload*X2)
Where:(a) X2 is Transformer turns ratio (X2 in all above examples is 4:1, 1/X2 = 0.25
(b) t1 is exponential decay time of filter capacitance and is equal to solution of
EXP(-t1/(Rload*C)) + Cos(2*π*fo*t1) = 0
One can solve using: HP49g+ calculator, Mathcad, MatLab, Excel Solver, etc.
(c) tw = 1/(2*fo) - t1
4c. i(t)RMS = Ipeak*(fo* tw*2/3)^0.5 For i(t) = ipeak*(1-t/tw)