Preamble
The subject of Op-Amp errors has been covered by many
writers. Dataforth’s Application Note 102 [1] covers the
topic as applied to instrumentation amplifiers and
provides links to spreadsheets for worst case error
analysis. This is a good place to go for the practical
engineer. The instrumentation amplifier of Application
Note 102 can be decomposed into the non-inverting
amplifier of this application note using Bartlett’s bisection
theorem [2].
Using circuit simulators and suitable Op-Amp macros
will provide quick results. Two free downloads are TI
Tina and LTspice. These may be found on the websites of
Texas Instruments and Linear Technology.
This note concerns only Op-Amps and does not attempt to
be exhaustive. Its objective is to show how final equations
of some basic errors are derived from first circuit
principles – primarily node analysis. Final equations are
enclosed with a box.
This Application Note is for the math driven reader. We
have all had the experience in our math and technical
education of reading a treatment of some topic where the
author introduces material and jumps to a final equation
stating “the derivation is left to the interested reader.”
Unless our teacher gave the derivation as an assignment,
most of us were not interested. Another hated statement is
“may be seen by inspection.” Not all students are
interested inspectors. It does have to be admitted that
many books would be much too long if not for these
shortcuts. It is also true that self-taught knowledge, while
frequently incomplete, often stays longer. Perhaps nonmath
oriented people never knew that following along
with pencil and paper is what makes math come alive. For
many, math becomes a blur of meaningless symbols,
mindless formula plugging, or even blind imitation.
An elegant way to do the following analysis is using Middlebrook’s Extra Element Theorem [3]
However, I start with basic circuit analysis and turn the algebraic
crank.
Offset Voltage
Assume the circuit of Figure 1 is the “Ideal Operational
Amplifier” except for offset voltage and finite open loop
gain.
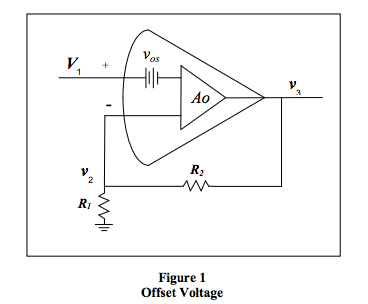
First, the ideal amplifier. For Αo to be very, very large,
the independent variable V1 must be close enough, for all
practical purposes, to the dependent variable ν2. To find
the Ideal Amplifier Gain, use the voltage divider relation:
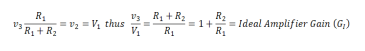
Negative feedback amplifiers are said to have closed loop
gain (Gcl). When the feedback connection is not made,
the phrase becomes open loop gain (Gol ). R1/R1 + R2 is
called the feedback factor. In this note Β symbolizes the
feedback factor.

Rearranging the terms,
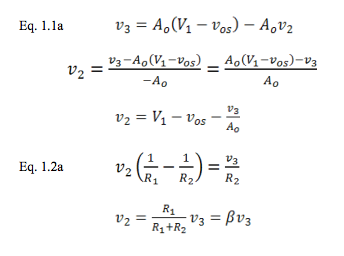
Combining Eq. 1.1a and Eq. 1.2a,
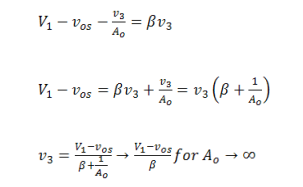

Equation 3 easily, perhaps eloquently, shows how offset
voltage and limited open loop gain modify the familiar
ideal gain equation. Modern Op-Amps have very high open loop gain. If , Αo → ∞ the error of offset voltage
alone is easily observed. It is multiplied by the closed
loop, ideal gain. This is often the most serious problem in
high gain Op-Amp applications.
Note that this is really basic feedback theory and applies
to much more than just Op-Amps. Some communication
amplifiers and various control problems are examples
with open loop gain far from infinite.
Bias and Offset Current
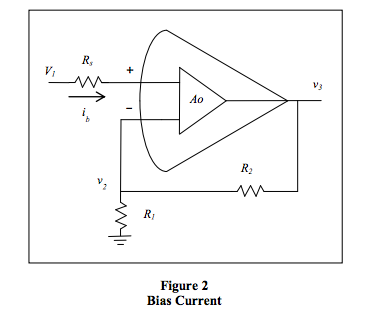

Eq. 2.1a and 2.2a
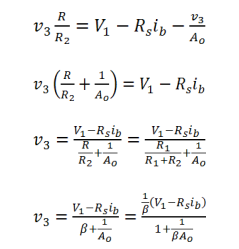
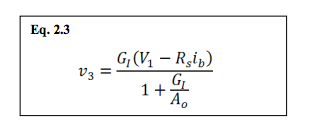
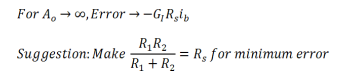
For many modern Op-Amp applications, the ideal model
is adequate. When it is not, consideration of offset voltage
and input current suffices for many of the rest.
Exceptions are high gain circuits and power amplifiers
driving a heavy load. Note that integrated circuit OpAmps
have almost equal bias currents on the positive and
negative inputs. The difference is sometimes called offset
or difference current. If the source resistances as seen
from each input are nearly the same, the error is
minimized.
The rest of this paper is for the interested reader. It has
more importance in general control systems.
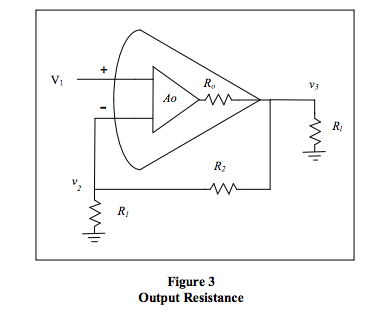
Output Resistance
The following amplifier is ideal in every way, except it
has limited open loop gain and a non-zero output
resistance. As we will see, if we assume infinite open loop
gain, the output resistance would have no effect. Since we
are considering non-zero output resistance, a load
resistance is included. Of course, the gain determining
resistors are also a load on the amplifier.
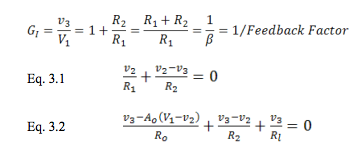
Gathering terms,
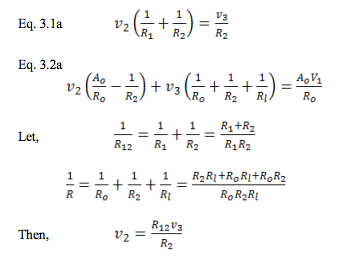
Combining equations,
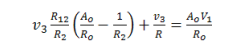
Or,
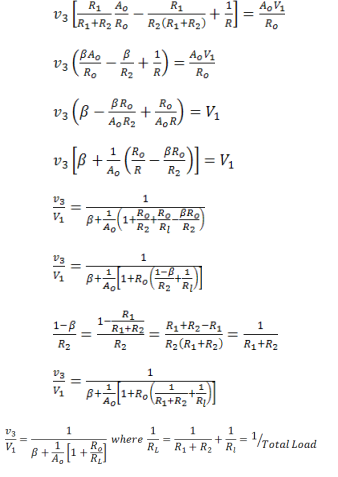
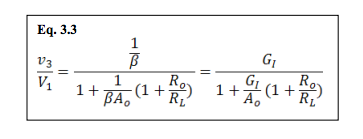
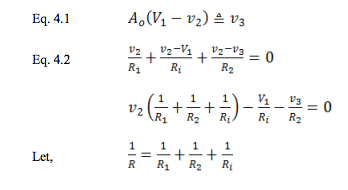
Rearranging terms,
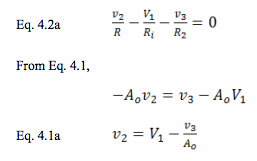
Combining equations 4.1a and 4.2a,
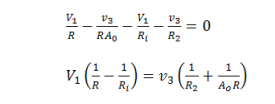
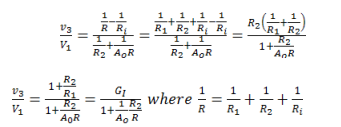

From equation 4.3, we can easily see how changes the
“ideal gain.” For infinite Αo, Ri has no effect
whatsoever. For that reason, we have to consider both in
the same model. This is intuitively satisfying from merely
looking at Figure 4. If we let Ri approach infinity, we get
the effect of Αo alone.
Now we can consider the input resistance of the entire
circuit.

From this we can see that the input resistance of the OpAmp
is increased by the ratio of open loop gain to the
closed loop, “ideal gain.” For example, using typical
values 105/102 = 103 gives an increase multiplier of
1000. Note that “ideal gain” is the inversion of the
feedback factor:
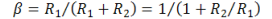
Some authors often use , rather than a symbol for “ideal
gain.”
Input, Output, and Load Resistance Altogether
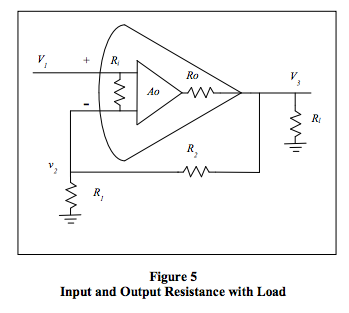
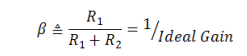
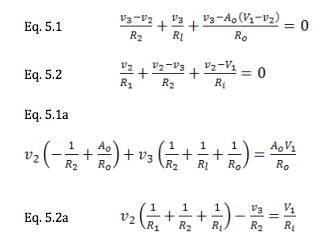
Define:
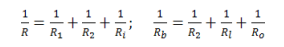
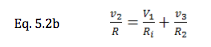
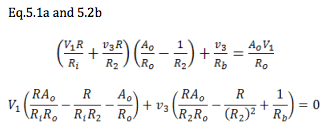
Now, we have a clear relation between the dependent
variable ν3 and the independent variable V1. At this
point, I will take the easy way out and say the next
intermediate steps are “left to the interested reader.” The
same algebraic methods of factoring and cancelling used
above will get you to Eq. 5.3. Remember as you go that Αo, Ri, and Rl
must be allowed to clearly approach
infinity. So put them in denominators so those terms will
approach zero. Ro must approach zero, so put it in
numerators. Finally look for any way that negative terms
can cancel out.

From equation 5.3, you may easily see how the amplifier
imperfections can go to their ideal limits leaving the ideal
gain equation, and there are no vexatious negative signs.
Equations with a negative sign cause me to wonder if the
whole thing could go negative. Then I have to ask myself
if that is physically meaningful or possible. If not, I may
have made a mistake. Last of all, don’t forget unit
analysis. Gain equations must have all terms unit-less,
voltages volts, resistances resistance, and so on. This is
often a quick way to see something is wrong, or going
wrong, in a derivation.

Example and Conclusion
Let’s see if any of this is worth considering. Consider the
following design.
Αo = 200k
Ri = 50kohm
Ro = 100
R2 = 99.9k
R1 = 100
Rl = 2k
These numbers in equation 5.3 yield a gain of 994.76, a
0.52% gain error. Almost all of this comes from the
denominator, and there only from Α0. A very slight
amount comes from the ratio Ro/Rl. I believe we could
also calculate an error for one element at a time and
assume superposition. Beyond this 0.5% error, the resistor
tolerances are obviously important. Offset voltage and
bias current may produce larger errors and should usually
be considered first. Additional error sources are noise,
power supply rejection, and common mode rejection.
Noise is a whole subject in itself. Then comes temperature
stability and ageing. Room temperature errors can be
calibrated out, but temperature and ageing cannot, unless
we use some type of reference and do automatic
calibration with a feedback loop. If we don’t have a
processor for this, a clocked feedback integrator with an
analog multiplexer can be used for offset error. Just
provide feedback to the ground connection of with R1 an
inverting integrator. Be careful of noise.
Perhaps for day-to-day work it is best to just use a good
simulation! However, always a however, while quick
numerical modeling is a great aid, we easily lose insight
into the sources of error. Equations like 5.3 can show
where the bulk of error comes from for a particular
application. In the example, almost all of the gain error
comes from the limited open loop gain and resistor
tolerances.
References
- Dataforth Application Note AN102
http://liwww.dataforth.com/catalog/pdf/an102.pdf
- Bi-section theorem: Bartlett, AC, “An extension
of a property of artificial lines,” Phil. Mag., Vol.
4, P902, Nov. 1927